Integration

(C) David Vajda
Sun Dec 22 10:26:24 2024
Uebungen fuer Integralrechnung und Extrema

6*x^6 + 6*x^6 + 3*x^1 + 7*x^3

12*x^6 + 3*x + 7*x^3

12*x^6 + 7*x^3 + 3*x

INT(12*x^6 + 7*x^3 + 3*x) = 12/7*x^7 + 7/4*x^4 + 3/2*x^2

Grenzen: b = 6
a = 2

F(6) - F(2)

F(6) = 12/7 * (6)^7 + 7/4 * (6)^4 + 3/2 * (6)^2
F(2) = 12/7 * (2)^7 + 7/4 * (2)^4 + 3/2 * (2)^2

F(6) = 12/7 * 279936 + 7/4 * 1296 + 3/2 * 36 = 479890.2857 + 2268 + 54 = 482212.2857
F(2) = 12/7 * 128 + 7/4 * 16 + 3/2 * 4 = 219.4285714 + 28 + 6 = 253.4285714

F(6) - F(2) = 481870.2857 - 253.4285714 = 481958.8571

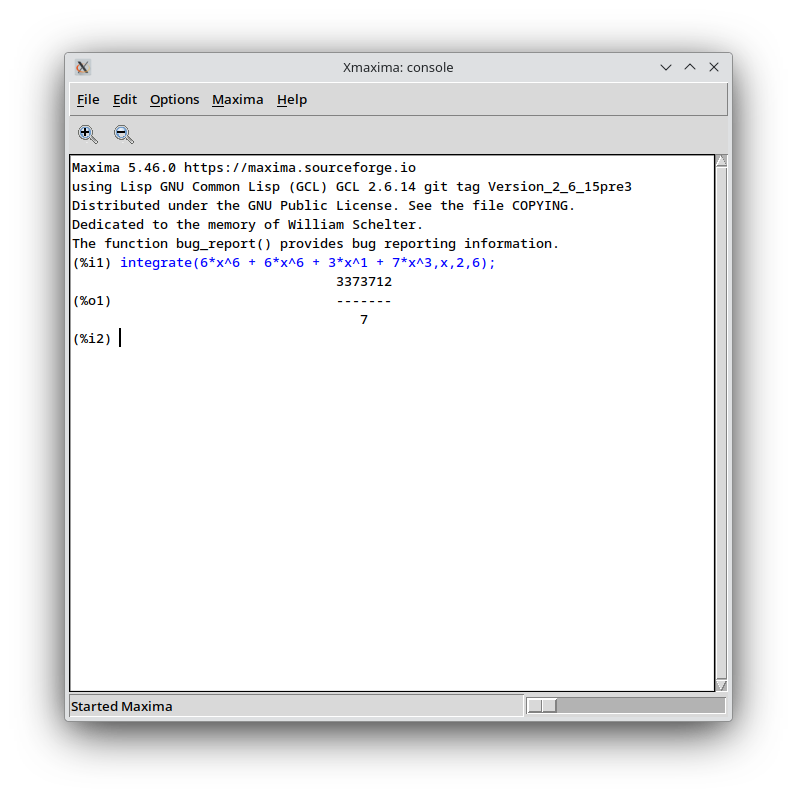
Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) integrate(6*x^6 + 6*x^6 + 3*x^1 + 7*x^3,x,2,6);
                                 3373712
(%o1)                            -------
                                    7
(%i2)

f(x) = 12*x^6 + 3*x + 7*x^3
f'(x) = (6*12)*x^5 + 3*7*x^2 + 3
f”(x) = (5*6*12)*x^4 + 2*3*7*x

f(x) = 12*x^6 + 3*x + 7*x^3
f'(x) = (6*12)*x^5 + 3*7*x^2 + 3 = 72*x^5 + 21*x^2 + 3
f”(x) = (5*6*12)*x^4 + 2*3*7*x = 360*x^4 + 42*x

Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
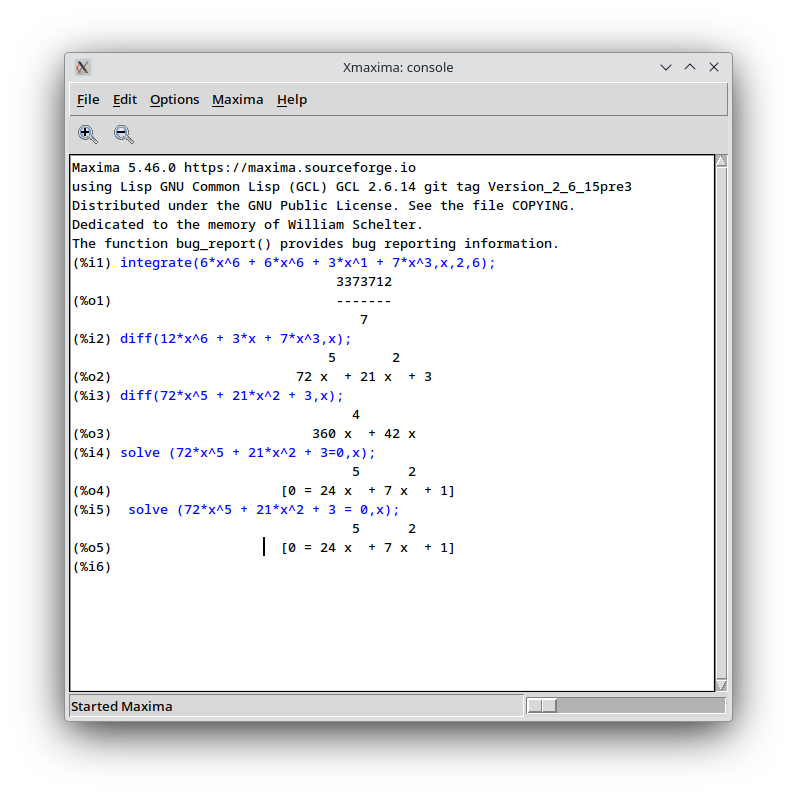
(%i1) integrate(6*x^6 + 6*x^6 + 3*x^1 + 7*x^3,x,2,6);
                                 3373712
(%o1)                            -------
                                    7
(%i2) diff(12*x^6 + 3*x + 7*x^3,x);
                                5       2
(%o2)                       72 x  + 21 x  + 3
(%i3) diff(72*x^5 + 21*x^2 + 3,x);
                                   4
(%o3)                         360 x  + 42 x
(%i4) solve (72*x^5 + 21*x^2 + 3=0,x);
                                   5      2
(%o4)                     [0 = 24 x  + 7 x  + 1]
(%i5)  solve (72*x^5 + 21*x^2 + 3 = 0,x);
                                   5      2
(%o5)                     [0 = 24 x  + 7 x  + 1]
(%i6)

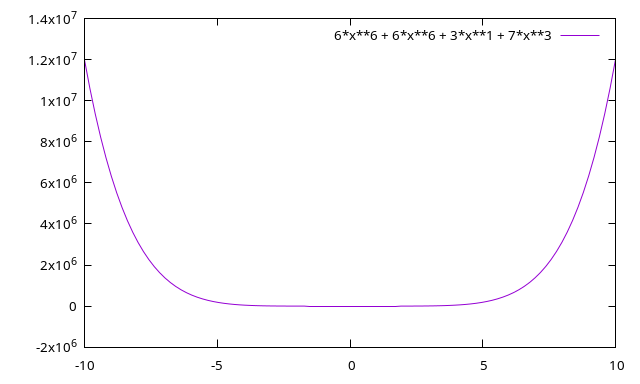
gnuplot

Richtig! Vorrausgesetzt, die Intervallgrenzen stimmen!

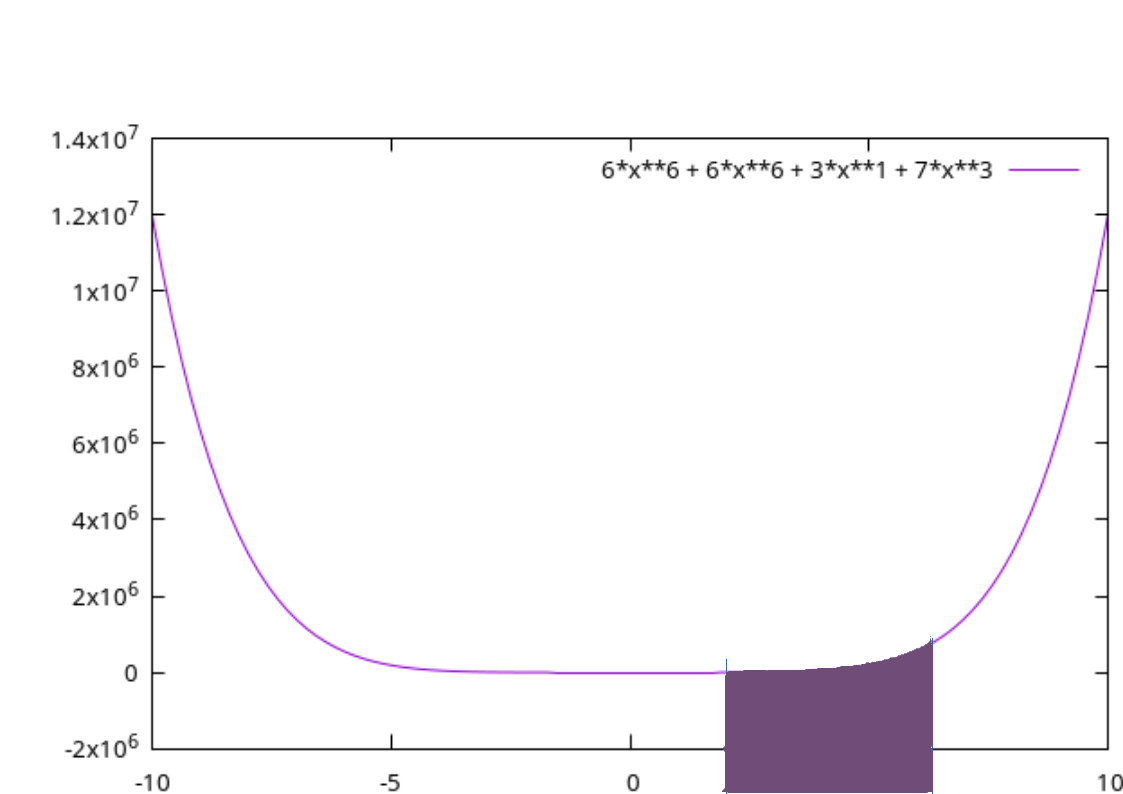
Falsch!

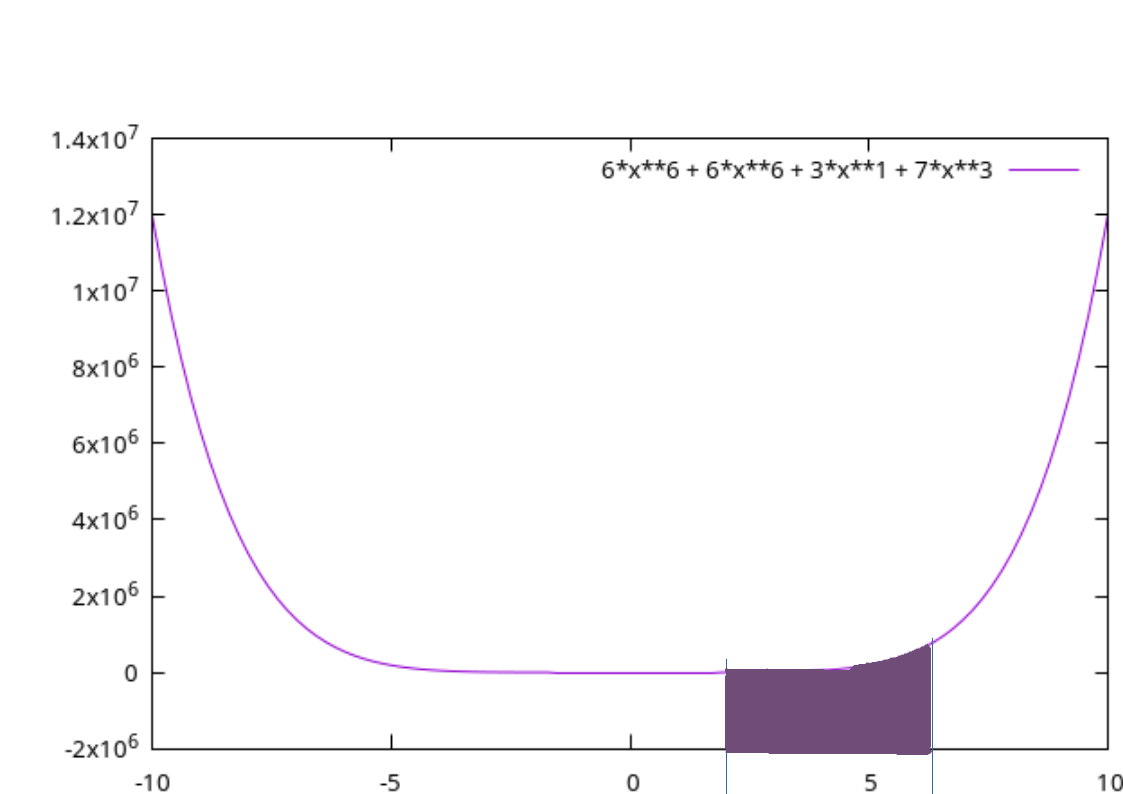
gnuplot> plot 6*x**6 + 6*x**6 + 3*x**1 + 7*x**3;
gnuplot>