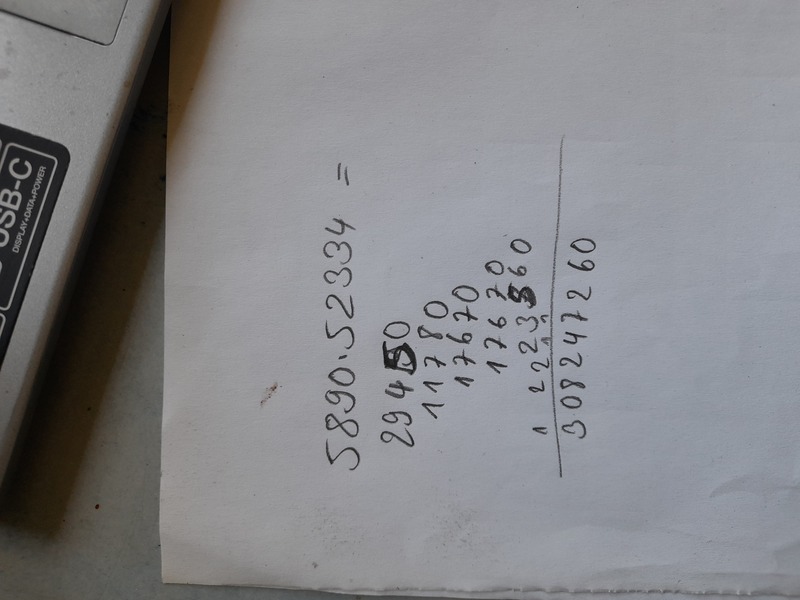Nächste Seite: Re: MySQL, Bash - Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Re: Graphs
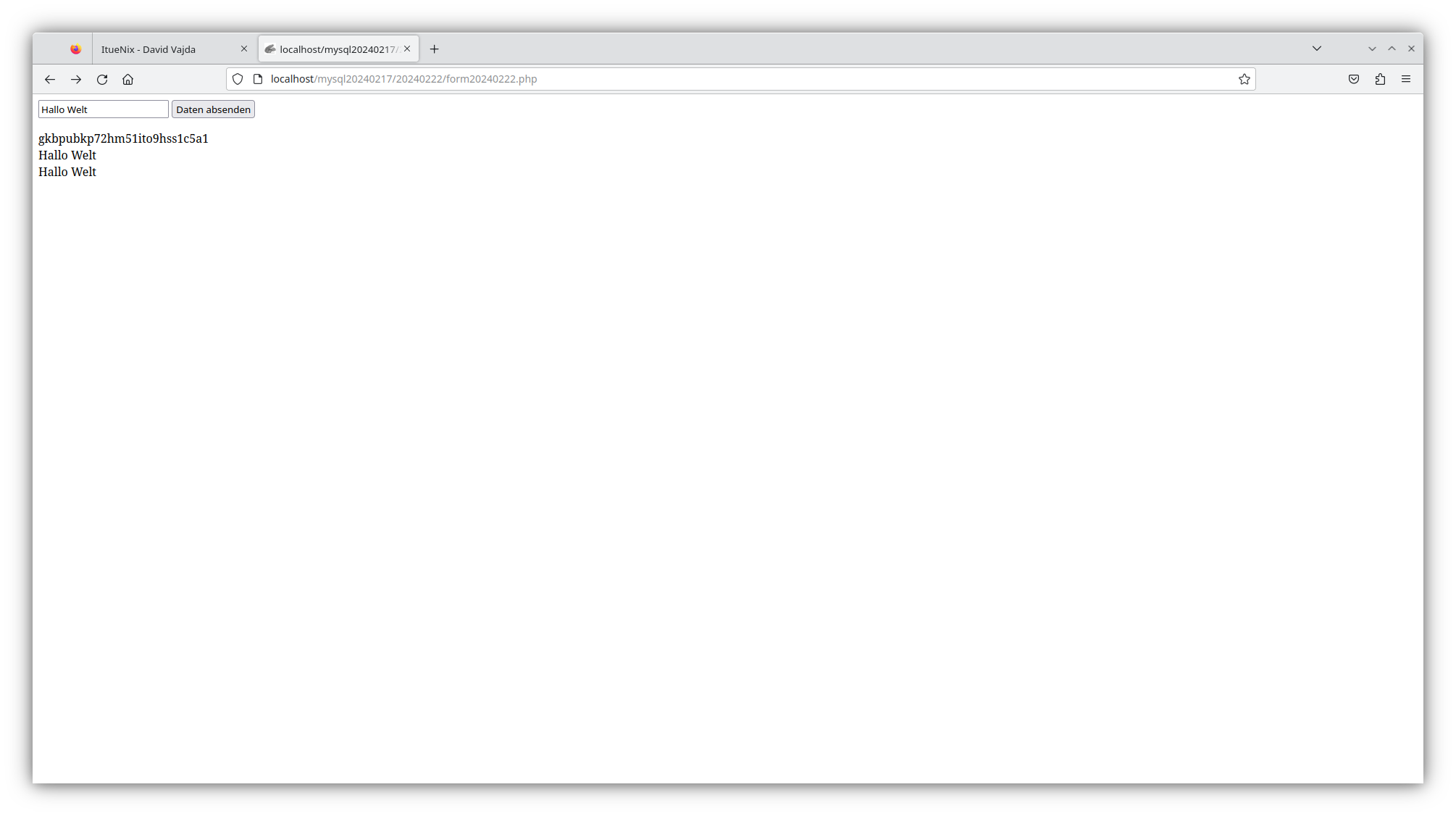
<?php
session_start ();
?>
<form method="POST" action="./form20240224.php">
<input type="text" name="2024022401"></input>
<input type="submit">
</form>
<?php
echo session_id () . "<br>n";
setcookie ("2024022402", "Hallo Welt, sagt Cookie 1", time () + 3600);
echo htmlentities (\$_POST ["2024022401"]) . "<br>n";
echo htmlentities (\$_COOKIE ["2024022402"]) . "<br>n";
echo htmlentities (\$_COOKIE ["2024022403"]) . "<br>n";
session_destroy ();
?>
POST http://localhost/mysql20240217/20240224/form20240224.php HTTP/1.1 host: localhost Cookie: 2024022403=Hallo Welt sagt Cookie 2 Content-Length: 31 Content-Type: application/x-www-form-urlencoded 2024022401=Ich bin Variable 1
Trying ::1... Connected to localhost. Escape character is '\^]'. HTTP/1.1 200 OK Date: Sat, 24 Feb 2024 12:13:28 GMT Server: Apache/2.4.57 (Debian) Set-Cookie: PHPSESSID=ipa52bt4n1vs6uovvrsp768em6; path=/ Expires: Thu, 19 Nov 1981 08:52:00 GMT Cache-Control: no-store, no-cache, must-revalidate Pragma: no-cache Set-Cookie: 2024022402=Hallo%20Welt%2C%20sagt%20Cookie%201; expires=Sat, 24 Feb 2024 13:13:28 GMT; Max-Age=3600 Vary: Accept-Encoding Content-Length: 217 Content-Type: text/html; charset=UTF-8 <form method="POST" action="./form20240224.php"> <input type="text" name="2024022401"></input> <input type="submit"> </form> ipa52bt4n1vs6uovvrsp768em6<br> Ich bin Variable 1 <br> <br> Hallo Welt sagt Cookie 2<br>
<?php
session_start ();
include ("/home/david/mysqldata.php");
\$db = new PDO ("mysql: host=localhost", \$MYSQL_USER, \$MYSQL_PASSWORD);
\$sql = "CREATE DATABASE mysql20240224" . session_id ();
\$db->query (\$sql);
\$sql = "USE mysql20240224" . session_id ();
\$db->query (\$sql);
\$sql = "CREATE TABLE a (x1 INTEGER, x2 INTEGER);";
\$db->query (\$sql);
\$sql = "CREATE TABLE b (y1 INTEGER, y2 INTEGER);";
\$db->query (\$sql);
\$sql = "INSERT INTO a (x1, x2) VALUES (4, 4);";
\$db->query (\$sql);
\$sql = "INSERT INTO a (x1, x2) VALUES (4, 8);";
\$db->query (\$sql);
\$sql = "INSERT INTO a (x1, x2) VALUES (8, 4);";
\$db->query (\$sql);
\$sql = "INSERT INTO a (x1, x2) VALUES (8, 8);";
\$db->query (\$sql);
\$sql = "INSERT INTO a (x1, x2) VALUES (9, 9);";
\$db->query (\$sql);
\$sql = "INSERT INTO b (y1, y2) VALUES (4, 8);";
\$db->query (\$sql);
\$sql = "INSERT INTO b (y1, y2) VALUES (8, 4);";
\$db->query (\$sql);
\$sql = "INSERT INTO b (y1, y2) VALUES (9, 9);";
\$db->query (\$sql);
\$sql = "SELECT x1, x2 FROM a;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt-> fetch())
echo \$row [0] . ", " . \$row [1] . "<br>n";
echo "<br>n";
\$sql = "SELECT y1, y2 FROM b;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . ", " . \$row [1] . "<br>n";
echo "<br>n";
\$sql = "SELECT x1, x2, y1, y2 FROM a INNER JOIN b;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . ", " . \$row [1] . ", " . \$row [2] . ", " . \$row [3] . "<br>n";
echo "<br>nn";
\$sql = "DROP DATABASE mysql20240224" . session_id ();
\$db->query (\$sql);
session_destroy ();
?>
4, 4<br> 4, 8<br> 8, 4<br> 8, 8<br> 9, 9<br> <br> 4, 8<br> 8, 4<br> 9, 9<br> <br> 4, 4, 4, 8<br> 4, 4, 8, 4<br> 4, 4, 9, 9<br> 4, 8, 4, 8<br> 4, 8, 8, 4<br> 4, 8, 9, 9<br> 8, 4, 4, 8<br> 8, 4, 8, 4<br> 8, 4, 9, 9<br> 8, 8, 4, 8<br> 8, 8, 8, 4<br> 8, 8, 9, 9<br> 9, 9, 4, 8<br> 9, 9, 8, 4<br> 9, 9, 9, 9<br> <br>
<?php
session_start ();
include ("/home/david/mysqldata.php");
\$db = new PDO ("mysql: host=localhost", \$MYSQL_USER, \$MYSQL_PASSWORD);
\$sql = "CREATE DATABASE q20240224" . session_id ();
\$db->query (\$sql);
\$sql = "USE q20240224" . session_id ();
\$db->query (\$sql);
\$sql = "CREATE TABLE a (x INTEGER);";
\$db->query (\$sql);
\$sql = "CREATE TABLE b (x INTEGER);";
\$db->query (\$sql);
\$sql = "CREATE TABLE c (x INTEGER);";
\$db->query (\$sql);
for (\$i = 0; \$i < 24; \$i++) {
\$sql = "INSERT INTO a (x) VALUES ("" . rand () % 32 . "");";
\$db->query (\$sql);
\$sql = "INSERT INTO b (x) VALUES ("" . rand () % 64 . "");";
\$db->query (\$sql);
\$sql = "INSERT INTO c (x) VALUES ("" . rand () % 48 . "");";
\$db->query (\$sql);
}
\$sql = "SELECT x FROM (SELECT x FROM a UNION SELECT x FROM b) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (SELECT x FROM a UNION SELECT x FROM c) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (SELECT x FROM b UNION SELECT x FROM c) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (SELECT x FROM a INTERSECT SELECT x FROM b) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (SELECT x FROM a INTERSECT SELECT x FROM c) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (SELECT x FROM b INTERSECT SELECT x FROM c) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM a UNION SELECT x FROM b) x
INTERSECT
SELECT x FROM c
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM a INTERSECT SELECT x FROM c) x
UNION
SELECT x FROM (SELECT x FROM b INTERSECT SELECT x FROM c) x
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM a UNION SELECT x FROM c) x
INTERSECT
SELECT x FROM b
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM a INTERSECT SELECT x FROM b) x
INTERSECT
SELECT x FROM (SELECT x FROM c INTERSECT SELECT x FROM b) x
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM b UNION SELECT x FROM c) x
INTERSECT
SELECT x FROM a
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "SELECT x FROM (
SELECT x FROM (SELECT x FROM b INTERSECT SELECT x FROM a) x
UNION
SELECT x FROM (SELECT x FROM c INTERSECT SELECT x FROM a) x
) x;";
\$stmt = \$db->query (\$sql);
while (\$row = \$stmt->fetch ())
echo \$row [0] . " ";
echo "<br>n";
\$sql = "DROP DATABASE q20240224" . session_id ();
\$db->query (\$sql);
session_destroy ();
?>
30 20 0 8 23 14 28 4 27 17 11 24 2 7 9 16 34 41 56 15 18 62 42 32 61 1 38 40 25 <br> 30 20 0 8 23 14 28 4 27 17 11 24 2 7 9 16 35 21 38 6 45 39 43 46 3 18 <br> 20 34 41 56 15 18 16 14 62 42 32 61 7 1 38 40 0 27 25 24 35 17 21 6 45 11 39 2 43 46 30 3 4 <br> 20 0 14 27 7 16 <br> 30 20 4 17 11 24 2 7 16 <br> 20 18 16 7 38 <br> 30 20 4 17 11 24 2 7 16 18 38 <br> 30 20 4 17 11 24 2 7 16 18 38 <br> 20 0 14 27 7 16 38 18 <br> 20 7 16 <br> 20 16 14 7 0 27 24 17 11 2 30 4 <br> 20 16 14 7 0 27 24 17 11 2 30 4 <br>
#!/bin/bash echo "Hallo Welt"
Hallo Welt
#!/bin/bash
i=0
while [ \$i -lt 10 ]
do
echo "Hallo \$((\$i+1))."
i=\$((\$i+1))
done
Hallo 1. Hallo 2. Hallo 3. Hallo 4. Hallo 5. Hallo 6. Hallo 7. Hallo 8. Hallo 9. Hallo 10.
#!/bin/bash
if [[ "\$1" == "David" \&\& "\$2" == "Vajda" ]]
then
echo "Das bin ich"
elif [ "\$1" == "David Vajda" ]
then
echo "Das bin ich"
elif [ "\$1" == "David" ]
then
echo "Das koennte ich sein"
elif [ "\$1" == "Vajda" ]
then
echo "Das koennte ich sein"
else
echo "Das bin ich nicht"
fi
#!/bin/bash /bin/bash ifthenelse.sh "David" "Vajda" >> ifthenelse.out /bin/bash ifthenelse.sh "David Vajda" >> ifthenelse.out /bin/bash ifthenelse.sh "David" >> ifthenelse.out /bin/bash ifthenelse.sh "Vajda" >> ifthenelse.out /bin/bash ifthenelse.sh "Max Mustermann" >> ifthenelse.out
Das bin ich Das bin ich Das koennte ich sein Das koennte ich sein Das bin ich nicht
#!/bin/bash
a=(Dies ist ein Array)
a+=(was man fortsetzen kann)
i=0
while [ \$i -lt 8 ]
do
echo "a [\$i] = \${a[\$i]}"
i=\$((\$i+1))
done
for s in \${a[@]}
do
echo "\$s\$i = \$s"
done
a [0] = Dies a [1] = ist a [2] = ein a [3] = Array a [4] = was a [5] = man a [6] = fortsetzen a [7] = kann \$s8 = Dies \$s8 = ist \$s8 = ein \$s8 = Array \$s8 = was \$s8 = man \$s8 = fortsetzen \$s8 = kann
#!/bin/bash
l=\$(ls)
for s in \$l
do
echo "\$s"
done
array.out array.sh cmd.out cmd.sh hello.out hello.sh ifthenelseexec.sh ifthenelse.out ifthenelse.sh while.out while.sh
0 0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 0
3 0 0 1 1 1
4 0 1 0 0 0
5 0 1 0 1 1
6 0 1 1 0 0
7 0 1 1 1 1
8 1 0 0 0 0
9 1 0 0 1 0
10 1 0 1 0 1
11 1 0 1 1 1
12 1 1 0 0 1
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1 1
1 0 0 0 1 1
3 0 0 1 1 1
5 0 1 0 1 1
7 0 1 1 1 1
10 1 0 1 0 1
11 1 0 1 1 1
12 1 1 0 0 1
13 1 1 0 1 1
14 1 1 1 0 1
15 1 1 1 1 1
Gruppe 1:
1 0 0 0 1 1
Gruppe 2:
3 0 0 1 1 1
5 0 1 0 1 1
10 1 0 1 0 1
12 1 1 0 0 1
Gruppe 3:
7 0 1 1 1 1
11 1 0 1 1 1
13 1 1 0 1 1
14 1 1 1 0 1
Gruppe 4:
15 1 1 1 1 1
1:3 0 0 - 1
1:5 0 - 0 1
3:7 0 - 1 1
3:11 - 0 1 1
5:7 0 1 - 1
5:13 - 1 0 1
10:11 1 0 1 -
10:14 1 - 1 0
12:13 1 1 0 -
12:14 1 1 - 0
7:15 - 1 1 1
11:15 1 - 1 1
13:15 1 1 - 1
14:15 1 1 1 -
5:13 - 1 0 1
7:15 - 1 1 1
3:11 - 0 1 1
1:5 0 - 0 1
3:7 0 - 1 1
10:14 1 - 1 0
11:15 1 - 1 1
1:3 0 0 - 1
5:7 0 1 - 1
12:14 1 1 - 0
13:15 1 1 - 1
10:11 1 0 1 -
12:13 1 1 0 -
14:15 1 1 1 -
Gruppe 2:
5:13 - 1 0 1
3:11 - 0 1 1
Gruppe 3:
7:15 - 1 1 1
5:13:7:15 - 1 - 1
3:11:7:15 - - 1 1
Gruppe 1:
1:5 0 - 0 1
Gruppe 2:
3:7 0 - 1 1
10:14 1 - 1 0
Gruppe 3
11:15 1 - 1 1
1:5:3:7 0 - - 1
3:7:11:15 - - 1 1
10:14:11:15 1 - 1 -
Gruppe 1:
1:3 0 0 - 1
Gruppe 2:
5:7 0 1 - 1
12:14 1 1 - 0
Gruppe 3:
13:15 1 1 - 1
1:3:5:7 0 - - 1
5:7:13:15 - 1 - 1
12:14:13:15 1 1 - -
10:11 1 0 1 -
12:13 1 1 0 -
14:15 1 1 1 -
10:11:14:15 1 - 1 -
12:13:14:15 1 1 - -
5:13:7:15 - 1 - 1
3:11:7:15 - - 1 1
1:5:3:7 0 - - 1
3:7:11:15 - - 1 1
10:14:11:15 1 - 1 -
1:3:5:7 0 - - 1
5:7:13:15 - 1 - 1
12:14:13:15 1 1 - -
10:11:14:15 1 - 1 -
12:13:14:15 1 1 - -
5:13:7:15 - 1 - 1
5:7:13:15 - 1 - 1
3:11:7:15 - - 1 1
3:7:11:15 - - 1 1
1:5:3:7 0 - - 1
1:3:5:7 0 - - 1
10:14:11:15 1 - 1 -
10:11:14:15 1 - 1 -
12:14:13:15 1 1 - -
12:13:14:15 1 1 - -
5:13:7:15 - 1 - 1
5:7:13:15 - 1 - 1
3:11:7:15 - - 1 1
3:7:11:15 - - 1 1
1:5:3:7 0 - - 1
1:3:5:7 0 - - 1
10:14:11:15 1 - 1 -
10:11:14:15 1 - 1 -
12:14:13:15 1 1 - -
12:13:14:15 1 1 - -
5:13:7:15 - 1 - 1
3:11:7:15 - - 1 1
1:5:3:7 0 - - 1
10:14:11:15 1 - 1 -
12:14:13:15 1 1 - -
1 3 5 7 10 11 12 13 14 15
5:13:7:15 * * * *
3:11:7:15 * * * *
1:5:3:7 * * * *
10:14:11:15 * * * *
12:14:13:15 * * * *
1 3 5 7 10 11 12 13 14 15
1:5:3:7 * * * *
10:14:11:15 * * * *
12:14:13:15 * * * *
1:5:3:7 0 - - 1
10:14:11:15 1 - 1 -
12:14:13:15 1 1 - -
y <= (not x3 and x0) or
(x3 and x1) or
(x3 and x2);
y <= (x3 or not x0) and
(not x3 or not x1) and
(not x3 or not x2);
library ieee;
use ieee.std_logic_1164.all;
entity quine20240224 is
port (
x3, x2, x1, x0: in std_logic;
y: out std_logic
);
end;
architecture behaviour of quine20240224 is
begin
y <= (not x3 and x0) or
(x3 and x1) or
(x3 and x2);
end;
library ieee;
use ieee.std_logic_1164.all;
entity quine20240224testbench is
port (
y: out std_logic
);
end;
architecture behaviour of quine20240224testbench is
component quine20240224
port (
x3, x2, x1, x0: in std_logic;
y: out std_logic
);
end component;
signal x3, x2, x1, x0: std_logic;
begin
q: quine20240224 PORT MAP (x3=>x3, x2=>x2, x1=>x1, x0=>x0, y=>y);
library ieee;
use ieee.std_logic_1164.all;
entity quine20240224 is
port (
x3, x2, x1, x0: in std_logic;
y: out std_logic
);
end;
architecture behaviour of quine20240224 is
begin
y <= (not x3 and x0) or
(x3 and x1) or
(x3 and x2);
end;
library ieee;
use ieee.std_logic_1164.all;
entity quine20240224testbench is
port (
y: out std_logic
);
end;
architecture behaviour of quine20240224testbench is
component quine20240224
port (
x3, x2, x1, x0: in std_logic;
y: out std_logic
);
end component;
signal x3, x2, x1, x0: std_logic;
begin
q: quine20240224 PORT MAP (x3=>x3, x2=>x2, x1=>x1, x0=>x0, y=>y);
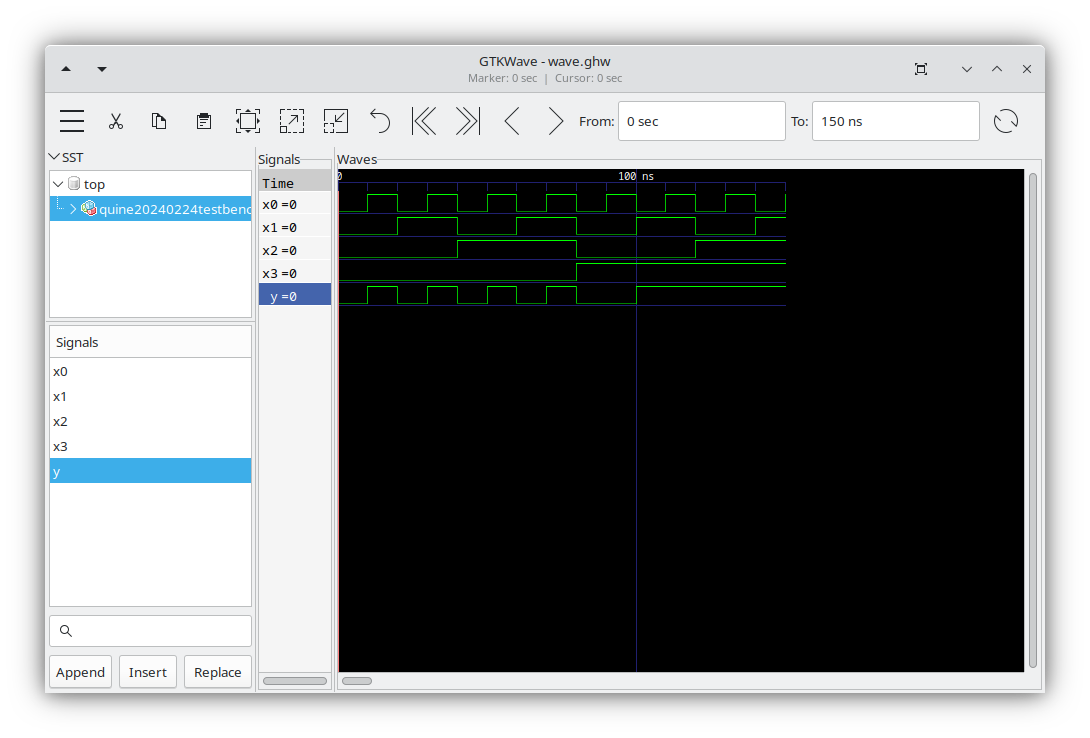
x0 <= '0' after 0 ns, '1' after 10 ns, '0' after 20 ns, '1' after 30 ns, '0' after 40 ns, '1' after 50 ns, '0' after 60 ns, '1' after 70 ns, '0' after 80 ns, '1' after 90 ns, '0' after 100 ns, '1' after 110 ns, '0' after 120 ns, '1' after 130 ns, '0' after 140 ns, '1' after 150 ns;
x1 <= '0' after 0 ns, '0' after 10 ns, '1' after 20 ns, '1' after 30 ns, '0' after 40 ns, '0' after 50 ns, '1' after 60 ns, '1' after 70 ns, '0' after 80 ns, '0' after 90 ns, '1' after 100 ns, '1' after 110 ns, '0' after 120 ns, '0' after 130 ns, '1' after 140 ns, '1' after 150 ns;
x2 <= '0' after 0 ns, '0' after 10 ns, '0' after 20 ns, '0' after 30 ns, '1' after 40 ns, '1' after 50 ns, '1' after 60 ns, '1' after 70 ns, '0' after 80 ns, '0' after 90 ns, '0' after 100 ns, '0' after 110 ns, '1' after 120 ns, '1' after 130 ns, '1' after 140 ns, '1' after 150 ns;
x3 <= '0' after 0 ns, '0' after 10 ns, '0' after 20 ns, '0' after 30 ns, '0' after 40 ns, '0' after 50 ns, '0' after 60 ns, '0' after 70 ns, '1' after 80 ns, '1' after 90 ns, '1' after 100 ns, '1' after 110 ns, '1' after 120 ns, '1' after 130 ns, '1' after 140 ns, '1' after 150 ns;
end;
Ach, ich weiss, was ich vergessen habe, ich wollte MIPS Assembler Code schreiben.
Jetzt ein Programm - was mit Shiften eine Zahl durch die andere teilt. Mit der Multiplikation hat es mit Shiften geklappt. Jetzt der Versuch das ganze zu invertieren.
Multiplikation 100 * 1100101 = 1100101 00 1000 * 1100101 = 1100101 000 10000 * 1100101 = 1100101 0000 100000 * 1100101 = 1100101 00000 101 * 1100101 = 1100101 00 + 1100101 1011 * 1100101 = 1100101 000 + 11001010 + 1100101 10101 * 1100101 = 1100101 0000 + 1100101 00 + 1100101 101100 * 1100101 = 1100101 00000 + 1100101 000 + 1100101 00 Jetzt wie geht es bei der Division Ich muss die Zahl nach Rechts shiften 1100101 00000 >> entsprechend des Divisors, ob 1 oder 0 nach rechts shiften Jetzt, wenn der Divisor einen kleineren Anteil enth"alt, muss ich den auch nach rechts shiften so habe ich lauter nach rechts geshiftete, nachher vom Dividenden ziehe ich das alles ab. Weil der Dividend ist ja eine Summe, die bei der Multiplikation entstanden ist. Ich probiere es zun"achst mal in C, weil das ist einfacher
Zunächst was zum Auswendig lernen, für den Herrn Vajda
Wie sie sehen, kann man sehr gut alte Schwächen tilgen, indem man auswendig lernt
little-Endian: "falsch rum" (intel-hex) big-endian: "richtig rum": 0xb54612a5 \^= 0xa51246b5 Im Intel Hex Format
Jetzt Dividend und Divisor ist schnell gelernt. Wenn man so lernt. Aber es ist lateinisch auch logisch. Ich hatte von der 5. bis zur 9. Klasse Latein. Es gibt die typischen Endungen, us, a - sie sehen mein Latein ist nicht so sehr das beste. us, a, um. Und dann gibt es - ich or. Oder wie?
A ja,
us (maskulinum) a (femininum) um (neutrum) er - ager (Der Boden, Acker) terror - terroris - der Schrecken furor - die Angst
Das sind so sachen, wie soll ich sagen, die klingen eher härter und gröber. Man sieht, mein Latein geht nicht mehr so gut
Für Informatiker nicht gut nicht zu wissen, wo nicht der Dividend steht und der Divisor
Aber, wenn man was nicht weiss, dann lernt man es. Deswegen studiert man. Und nicht nur das. Das ist Wissenschaft. Wissenschaft heisst nicht die tollsten Dinge wissen, die man nicht wissen kann, aber besonders nicht begründen kann, wissenschaft heisst das genau zu kennen, was eindeutig erwiesen ist
Also, da habe ich noch was. Bei der Multiplikation heisst das Mulitplikant und Multiplikator. Das ist logisch.
Multi lateinisch viel. dividere teilen. Addere dazu geben. Ad - dazu. Dare geben. Substrahere - abziehen. Sub unter, trahere - kontraktion ziehen. Gut - aber - bei der Prozentrechnung fehlt es bei mir noch. Bei der Zinsrechnung nicht die Rechnung, das ist logisch. sondern die Namen.
Dann Prozent geht mir gerade zu weit
Prozentwert Grundwert Prozentsatz Prozentfuss
Sehen sie, ich finde die Seite gerade nicht, die ich gefunden hatte, wo ich fand, dass es gut drauf steht. Aber das ist mir jetzt egal
Weil ich lerne
Dividend Divisor - Quotient Multiplikant Multiplikator - Produkt
Jetzt werden sie fragen, warum ich beim Prozent nicht lange suche. Ich will mir jetzt alles erklären. Nein, ich erkläre nichts. Manche sachen. Ach, das haben sie jetzt nicht. Dann suchen sie ewig bei Prozentwert und gehen zu Euklid und können sich am Ende nichts erklären.
Wissen sie, sagen wir, die Lerneinheit besteht aus
50:50
50
Prozentwert
Grundwert
Prozentsatz
Prozentfuss
Grundrechenarten:
Addition
Subtraktion
Multiplikation
Division
Grundrechenarten!
Addition
Summand + Summand = Summenwert
Addition
Summand
Summenwert
Subtraktion
Minuend - Subtrahend = Differenzwert
Minuend
Subtrahend
Differenzwert
Multiplikation
Multiplikator * Multiplikand = Produktwert
Multiplikator
Multiplikand
Produktwert
Division
Dividend:Divisor = Quotientwert
Dividend
Divisor
Quotientwert
Spr"uche:
Summand vorne und hinten
Minuend vorne Subtrahend hinten
Dividend vorne Divisor unten
Multiplikator vorne, Multiplikand hinten
Prozentwert Grundwert Prozentsatz Prozentfuss
Grundrechenarten: Addition Subtraktion Multiplikation Division
Grundrechenarten!
Addition Summand + Summand = Summenwert
Addition Summand Summenwert
Subtraktion Minuend - Subtrahend = Differenzwert
Minuend Subtrahend Differenzwert
Multiplikation Multiplikator * Multiplikand = Produktwert
Multiplikator Multiplikand Produktwert
Division Dividend:Divisor = Quotientwert
Dividend Divisor Quotientwert
Sprüche: Summand vorne und hinten Minuend vorne Subtrahend hinten Dividend vorne Divisor unten Multiplikator vorne, Multiplikand hinten
Ach ja, das ist Teil der Übungen. Das habe ich vergessen
Ich muss noch machen
// Geniale Formel zum Binomialkoeffizient
p = 1;
q = 1;
for (i = 0; i < k; i++) {
p = p * (n-i);
q = q * (i+1);
}
// eventuell kleiner Rechenfehler drin, muss noch verifiziert werden
Der Binomialkoffizient wirkt als Formel kompliziert. Aber es gibt zwei Formeln. Habe ich in Algo Mathematik erfahren.
(n C r)
Also. Fakultät ist einfach
Eine der einfachsten Reihen ist
1+2+3+4+5+...+n
SUM_{i=1}\^n i
Gut, das lässt sich in der Programmierung einfach ausdrücken als
s = 0 for (i = 1; i <= n; i++) s = s + i;
Ebenso einfach die Fakultät
p = 1; for (i = 1; i <= n; i++) p = p * i;
Jetzt gibt es die Standardformel für den Binomialkoeffizient, die finde ich nicht so easy.
Zuhnächst geht der
(n(n-1)(n-2)* ... * (n-k+1))/(1*2*...*(k-1)*k)
Das ist jetzt nicht die Formel. Sondern die Definition. Oder wie man sagen solll
OK, das ist einfach. Das im divisor ist einfach
k!
Und das oben ist etwas wie n! allerdings - mit dem Unterschied dass es wie wenn man Summen subtrahiert nur bis k geht
Also, ich finde die Formel gut
(PROD_{i=0}\^{k-1}(n-i)/k!
Das finde ich gut, dann kommt das Programm raus.
Also, was mir fehlt
Assembler Code MIPS32 IEEE754 Umrechnung, jeden Tag Grundrechenarten, jeden Tag
Das bedeutet, ich schreibe jetzt erst das C Programm zur Division
Ich schreibe jetzt ein C Programm zur Diviosn und Multiplikation - von Binärzahlen, ohne zu teilen, nur mit Shiften Addieren und Subtrahieren. In MIPS32 Assembler habe ich eines zur Multiplikation geschrieben, das tut
Jetzt noch mal, aber in C.
Warum sich das lohnt ist einfach. weil sie einfach ein Multiplizierschaltnetz bauen können. Und wie das geht, ist jetzt klar
Sie geben den Multiplikator mehrfach ein
Also, wenn sie den Multiplikanden
>100haben
Dann geben sie den Multiplikator binär ein. Den müssen sie nicht schieben. sie brauchen keinen Shifter, sie brauchen kein Schaltwerk. ein Schaltetz reicht. Sie haben
Bit a3, a2, a1, a0 f"ur den Multiplikator
Und wenn sie mit einer 4 Stelligen Binärzahl multiplizieren, hängen sie hinten 4 Nullen an
a3, a2, a1, a0, 0, 0, 0, 0
das ganze machen sie, noch mal
0, a3, a2, a1, a0, 0, 0, 0 0, 0, a3, a2, a1, a0, 0, 0 0, 0, 0, a3, a2, a1, a0, 0
0, 1, hochohmig schalten
c1 = a and b c2 = a or b
// Ich weiss, wo der Fehler ist, ich habe es schon richtig gemacht nur
// ich muss mit dem h"ochsten Bit anfangen, bei dieser Art der Subtraktion und nicht anders herum.
#include <stdio.h>
int main (void) {
int divisor = 4;
int dividend = 123782;
int quotient;
int produkt;
int multiplikator = 123782;
int multiplikant = 1231;
int i;
int div2;
produkt = 0;
for (i = 0; i < 16; i++)
if ((multiplikant >> i) \& 0x01)
produkt = produkt + (multiplikator << i);
printf ("produkt %in", produkt);
printf ("produkt ueber computer %in", multiplikant * multiplikator);
quotient = dividend;
for (i = 0; i < 16; i++)
if ((divisor >> i) \& 0x01)
quotient = quotient - (dividend >> i);
printf ("quotient: %in", quotient);
printf ("quotient, originale: %in", dividend/divisor);
return 0;
}
Nein, das stimmt auch nicht. Das ist jetzt letzten Endes egal.
Also, drehen wir mal die Multiplikation um Wir haben ein Ergebnis. das ist c Und wenn wir mit 101 multiplizieren. Dann haben wir c = x * 100 + 1 * x Das heisst, wir m"ussen - ach so, jetzt sehe ich. Dann ergibt das so keinen Sinn. Wahrscheinlich Jetzt ist unser Dividend das Ding. Kurz nachdenken, raucherpause. Sie wissen ja nicht mit was. Das heisst, sie haben eine Gleichung Das 100 und das 1. Haben wir trotzdem. Der Dividend - ist zwar ein Produkt von einer anderen Multiplikation. Und wird jetzt durch einen Divisor geteilt, das eine andere Operation ist. das heisst eine andere Division. Trotzdem entspricht unserem Multiplikanden Und x entspricht unserem Multiplikator. x ist der Multiplikator Und 101 ist der Divend - der Multiplikand. Jetzt m"ussen wir eine Gleichung l"osen.
Jetzt kommen wom"oglich ohne das Beabsichtigt zu haben, der Analytical Machine schon ganz nahe. Das ist eine Gleichung. Die k"onnten wir im Horner scheme aufschreiben. Wenn wir mit (111)*x = 100 * x + 10 * x + 1 *x 10 * ( 10x + x) + x Doch das ist so. Also, probieren wir es zur Sicherheit aus 100 * xb = x00b 1000 * xb = x000b Und jetzt wenn wir mit 111 x00b + x0b +xb = c Das heisst, c = xb*100b + xb*10b + xb (xb*10b + xb) 10b + xb Gut, dann ist es wenigstens nicht trivial, wir haben uns mal gedanken gemacht und erkannt es nicht ist nicht trivial. wenn das nicht gelingt, das nicht zu l"osen, ist das kein Beinbruch. Wenn es gelingt es zu l"osen, diese gleichung, um so besser.
Macht nichts, dann mache ich jetzt pause und mache mein Übungsprogramm weiter. Da sind noch Fehler drin, was den Bereich betrifft. Und dann Übungen
IEEE-754-Std
Und dann mache ich vorher so eine Aufgabe.
12.78125 12/2 = 6 Rest 0 6/2 = 3 Rest 0 3/2 = 1 Rest 1 1/2 = 1 Rest 1 1100 0.78125 * 2 = 1.56250 1 0.56250 * 2 = 1.1250 1 0.125 * 2 = 0.25 0 0.25 * 2 = 0.5 0 0.5 * 2 = 1.0 1 0.78125 0.78125 ------- 1.56250 0.56250 0.56250 ------- 1.1250 1100,11001 Shift 3 nach links 1100,11001b = 1,10011001b 127 + 3 = 130 130 / 2 = 65 Rest 0 65 / 2 = 32 Rest 1 32 / 2 = 16 Rest 0 16 / 2 = 8 Rest 0 8 / 2 = 4 Rest 0 4 / 2 = 2 Rest 0 2 / 2 = 1 Rest 0 1 / 2 = 0 Rest 1 10000010 1,10011001b normalisierung 10011001b [0][10000010][10011001] 0100.0001.0100.1100.1 0100.0001.0100.1100.1000.0000.0000 0x414C800
1.) Rechne die Zahl in binaer Darstellung in eine Dezimale Darstellung um
0010010011110111b 9463d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
65457 1111111110110001
3.) Addiere die drei Zahlen schriftlich
50202
+ 7202
+ 55609
-----------------
113013
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
42689
- 5746
- 4186
- 12073
-----------------
20684
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
-60 -68 = -128
11000100 10111100 = 10000000
6.) Multipliziere die zwei Zahlen schriftlich
5890*52334 = 308247260
7.) Dividiere die zwei Zahlen schriftlich
44137/17106 = 2
8.) Errechne x Logarithmisch mit dem Taschenrechner
1899\^x = 1821233251