Re: MySQL, Bash - Übungen

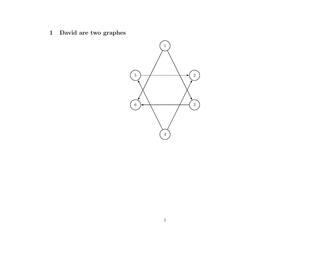
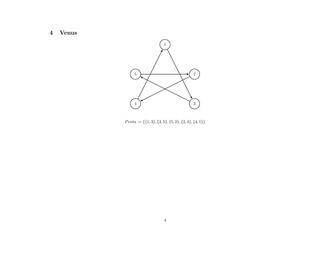
Penta := {{1,3},{3,5},{5,2},{2,4},{4,1}}

(a_0) = 1
(a_(n+1)) := (a_n)
(a_(n+2)) := (a_(n+1))

bis max. Und dann

(a_max) = 2
(a_(n+1)) := (a_n)
(a_(n+2)) := (a_(n+1))

1.) Rechne die Zahl in binaer Darstellung  in eine Dezimale Darstellung um
0001101110111100b 7100d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
14547 0011100011010011
3.) Addiere die drei Zahlen schriftlich
            12520
+           53156
+            1731
-----------------
            67407
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
            25863
-           13112
-           10486
-            8160
-----------------
            -5895
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
28 -59 = -31
00011100 11000101 = 11100001
6.) Multipliziere die zwei Zahlen schriftlich
43048*58395 = 2513787960
7.) Dividiere die zwei Zahlen schriftlich
28368/61974 = 0
8.) Errechne x Logarithmisch mit dem Taschenrechner
27844\^x = 1578605345

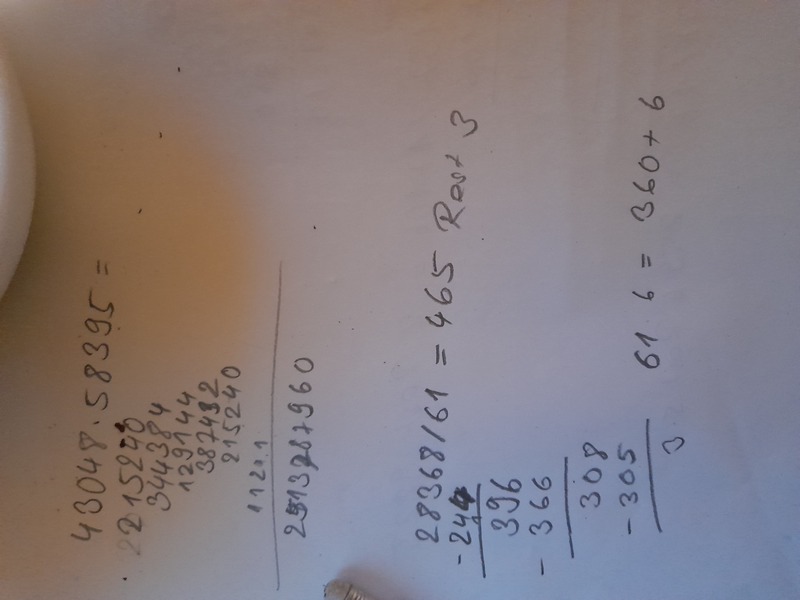
1.) Rechne die Zahl in binaer Darstellung  in eine Dezimale Darstellung um
1000011010011001b 34457d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
64763 1111110011111011
3.) Addiere die drei Zahlen schriftlich
            36403
+           37797
+           52811
-----------------
           127011
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
            17033
-            6948
-            8346
-            8821
-----------------
            -7082
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
-92 -60 = -152
10100100 11000100 = 01101000
6.) Multipliziere die zwei Zahlen schriftlich
7586*43888 = 332934368
7.) Dividiere die zwei Zahlen schriftlich
61163/6997 = 8
8.) Errechne x Logarithmisch mit dem Taschenrechner
10189\^x = 1627004107