20250918

load(interpol);p:[[1,2],[2,3],[4,4],[5,2], [6,5]]; f(x):=lagrange(p); expnd1f1: expand(f(x)); int1f1: integrate(f(x),x,1,6); plot2d(f(x),[x,1,6],[png_file,"/home/david/langrage20250918.png"]); tex (int1f1,"/home/david/langrage20250918.tex"); tex (expnd1f1,"/home/david/langrage20250918.tex");

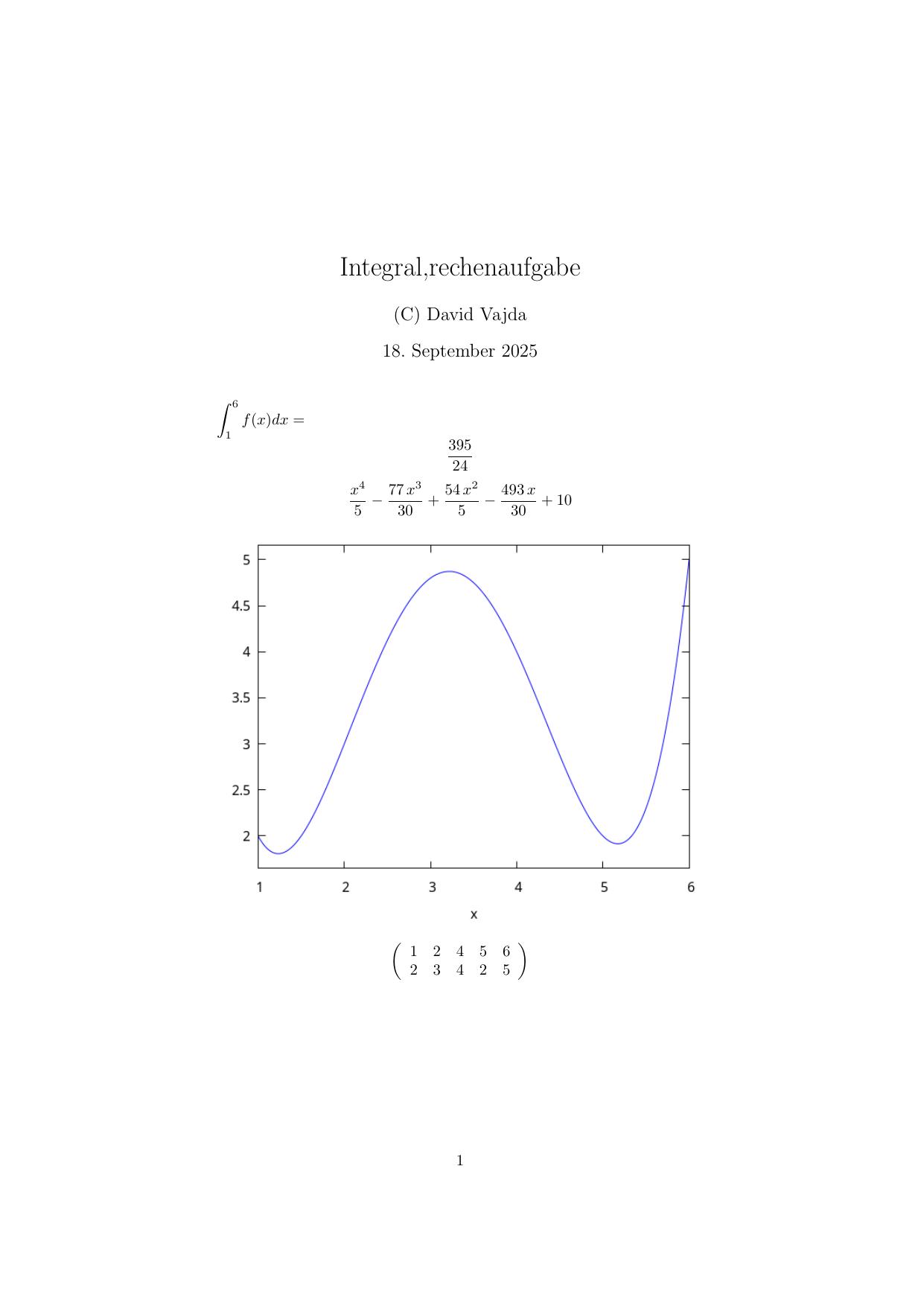
\documentclass[a4paper]{article} \usepackage{graphicx,german,amsmath,amsfonts} \author{(C) David Vajda} \title{Integral,rechenaufgabe} \begin{document}\maketitle $\displaystyle\int_{1}^{6}f(x)dx = $ 
$${{395}\over{24}}$$
$${{x^4}\over{5}}-{{77\,x^3}\over{30}}+{{54\,x^2}\over{5}}-{{493\,x
 }\over{30}}+10$$
\includegraphics[width=\textwidth]{/home/david/langrage20250918.png} $$\left(\begin{array}{ccccc}
1 & 2 & 4 & 5 & 6\\
2 & 3 & 4 & 2 & 5
\end{array}\right)$$ \end{document}

GAL16V8
RIPPLECARRYCHAINADDER20250918DAVIDVAJDA

C0      A4   B4   A3   B3    A2    B2    A1    B1       GND
/OE     S4   S3   S2   S1    C4    NC    NC    NC       VCC

; S = A XOR B XOR C
; U = A AND B OR (A OR B) AND C

S1      =       A1 $ B1 $ C0;
U1      =       A1 & B1 # (A1 # B1) & C0;

S2      =       A2 $ B2 $ U1;
U2      =       A2 & B2 # (A2 # B2) & U1;

S3      =       A3 $ B3 $ U2;
U3      =       A3 & B3 # (A3 # B3) & U2;

S4      =       A4 $ B4 $ U3;
C4      =       A4 & B4 # (A4 # B4) & U3;

DESCRIPTION
A RIPPLE CARRY CHAIN ADDER 20250918 DAVID VAJDA