2024-12-15, Mathematik

https://uebungsaufgaben.eu/bestimmte_integrale/ ich mache hier nachher die Aufgaben, ich tue sie zu den Standardaufgaben, die ich jeden Tag mache und gucke nach weiteren und mache sie jeden Tag. Unterschied: Ich mache dazu immer Zeichnung

Integral

https://uebungsaufgaben.eu/bestimmte_integrale/

INT_0^3(3*x^3+5)

INT(x^n) = (1/(n+1)*x^(n+1))

INT(3*x^3) = (3/4)*x^4
INT(5) = INT (5*x^0) = 5/1*x^1

INT_0^3(3*x^3+5) = F(3)-F(0) = (3/4)*3^4 + 5*3 = 75,75

$$\displaystyle\int{3\cdot x^3+5}, \displaystyle\int{x^n} = \dfrac{... ...e\int_0^3{3\cdot x^3+5} = F(3)-F(0) = \dfrac{3}{4}\cdot 3^4 + 5\cdot 3 = 75,75$$

jetzt habe ich in meinem Funktionsplotter den ich selber gemacht habe, kein Gradnetz aber ich kann gnuplot nehmen

(C) david vajda
2024-12-15
integral Aufgabe

f(x) = 2*x^3 + 4*x^2 + 7
INT_1^5 (f(x))

INT(2*x^3 + 4*x^2 + 7) = 2/4 * x^4 + 4/3 * x^3 + 7*x

F(5) = 2/4 * 5^4 + 4/3 * 5^3 + 7*5 = 312,5 + 166,666666667 + 35  = 514,166666667
F(1) = 2/4 * 1^4 + 4/3 * 1^3 + 7*1 = 0.5 + 1,3333 + 7 = 8,83333333334

F (b) - F (a) = 514,166666667 - 8,83333333334 = 505,333333334

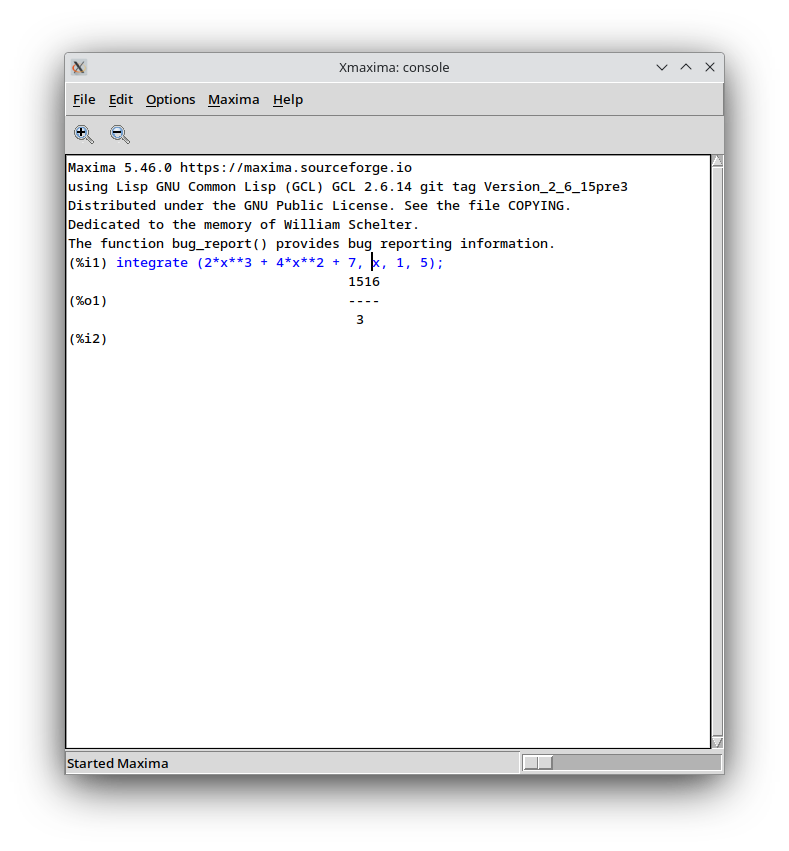
Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) integrate (2*x**3 + 4*x**2 + 7, x, 1, 5);
                                   1516
(%o1)                              ----
                                    3
(%i2)

Im oszilloskop ist die Flaeche unter der vom Oszilloskop eingezeichneten Funktion - generell die verrichtete Arbeit W = U*I*t. Das bestimmte Integral im Oszilloskop ist die Arbeit, dabei wird die Spannung U angezeigt, mit dem Strom verhaelt es sich: I=U/R, nach dem Ohmschen gesetz: R = U/I. Dabei verhaelt sich ein blindwiderstand wohl als linearer Wirkwiderstand, also, ein Widerstand wie wir ihn kennen. damit koennen wir I ausrechnen, was uns fehlt, wofuer wir R, als Impedanz in der gemessenen Schaltung kennen muessen allerdings muessten wir bedenken, dass der Strom beim Blind und Scheinwiderstand der Spannung vorauseilen kann...

Im oszilloskop ist die Flaeche unter der vom Oszilloskop eingezeichneten Funktion - generell die verrichtete Arbeit W = U*I*t. Das bestimmte Integral im Oszilloskop ist die Arbeit, dabei wird die Spannung U angezeigt, mit dem Strom verhaelt es sich: I=U/R, nach dem Ohmschen gesetz: R = U/I. Dabei verhaelt sich ein blindwiderstand wohl als linearer Wirkwiderstand, also, ein Widerstand wie wir ihn kennen. damit koennen wir I ausrechnen, was uns fehlt, wofuer wir R, als Impedanz in der gemessenen Schaltung kennen muessen
allerdings muessten wir bedenken, dass der Strom beim Blind und Scheinwiderstand der Spannung vorauseilen kann...

ich mache eine integrieraufgabe und eine matrizenmultiplikation. Um die Integrieraufgaben zu verschoenern, sie wissen, es sind Compiler auf meiner Homepage fuer arithmetische Ausdruecke. Und ich habe mal einen geschrieben, der das gegenteil tut, der ist auch noch da. Keine ausdruecke abarbeiten, zufaellig welche erzeugen. Das eignet sich fuer das Integrieren - weil - jetzt kriege ich schoene Klammerausdruecke.Wirklich? Fuer das Integrieren eignen sich am Besten Potenzfunktionen.Warum? Klammerausdruecke sind nicht einfach zu integrieren - weil so einfach sind die Integrationsregeln nicht an zu wenden, wie bei der Differenzierung Aber keine Panik - man kann die Klammern aufloesen Gut, ein Problem, ich schreibe das Programm nach einer kurzen Integration und einer Matrizenmultiplikation neu - die Ausdruecke duerfen nicht zu lang sein. Man muss sie fruehzeitig genug abbrechen und noch etwas: Das werden zu meinen ueblichen Aufgaben die Standardaufgaben, keine Sorge, ich uebertreibe nicht. Ich mache aber zu den Standardaufgaben, Matrizenmultiplikation ist ja schon dabei. Jeden Tag integrieren, ist nicht sehr schwer, und: Ich habe dann ja eine Funktion - die kann ich gleich auf Extrempunkte untersuchen, Minima, Maxima. Zur not einfach in das Computer Algebra System Maxima eingeben - und - dann findet es selber die Nullstellen

Sie muessen keine Sorge haben, ich uebertreibe nicht. Zu den bisherigen aufgaben der Digitaltechnik, ich mache MIPS32, weiter und KNF/DNF VHDL Quine Mc Cluskey, Automaten, ...

$$m = 4,n = 4,s = 4, \left(\begin{array}{ccccc}2&7&5&2&\\ 7&0&0&4&... ...&50&\\ 26&21&30&62&\\ 65&75&134&85&\\ 57&80&95&90&\\ \par\end{array}\right)$$

(C) David Vajda
2024-12-14
Matrixmultiplikation

(1:1) 2*2 + 7*3 + 5*3 + 2*3
= 4 + 21 + 15 + 6 = 10 + 36 = 46 Korrekt
(1:2) 2*3 + 7*2 + 5*9 + 2*0
6+14+45 = 65 korrekt
(1:3) 2*2 + 7*9 + 5*5 + 2*4
4+63+25+8 = 88 + 12 = 100
(1:4) 2*6 + 7*4 + 5*0 + 2*5
12+28+10 = 50
(2:1) 7*2 + 0 * 3 + 0 * 3 + 4 * 3
= 14+12 = 26
(2:2) 7*3 = 21
(2:3) 7*2 + 4*4 = 30
(2:4) 7*6 + 4*5 = 42+20 = 62
(3:1) 4*2 + 9*3 + 5*3 + 5*3
= 8 + 27 + 30 = 65
(3:2) 4*3 + 9*2 + 5*9
= 12 + 18 + 45 = 75
(3:3) 4*2 + 9*9 + 5*5 + 5*4
8 + 81 + 25 + 20
= 45 + 89 = 134
(3:4) 4*6 + 9*4 + 5*5
24 + 36 + 25 = 85
(4:1) 9*2 + 4*3 + 5*3 + 4*3
18 + 12 + 15 + 12
30 + 27 = 57
(4:2) 9*3 + 4*2 + 5*9
27 + 8 + 45 = 80
(4:3) 9*2 + 4*9 + 5*5 + 4*4
18 + 36 + 25 + 16
52 + 43 = 95
(4:4) 9*6 + 4*4 + 4*5
54 + 16 + 20
= 90

ok, jetzt integretation, dann der Compilergenerator fuer Funktionen zum integrieren, Extremwerte.

(C) David Vajda
Integration - Nr. 2
2024-12-14

f(x) = 5*x^3 + 2*x^4 + 1

INT_1^6 (f(x))

F(x) = 5/4 * x^4 + 2/5 * x^5 + x

F(b) = F(6) =
1.25 * 6^4 + 0.4 * 6^5 + 6 = 4736.4

F(a) = F(1)

1.25 * 1^4 + 0.4 * 1 + 1 =
1.25 + 0.4 + 1 = 2.65

F(6) - F(1) = 4736.4 - 2.65 = 4733.75

Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
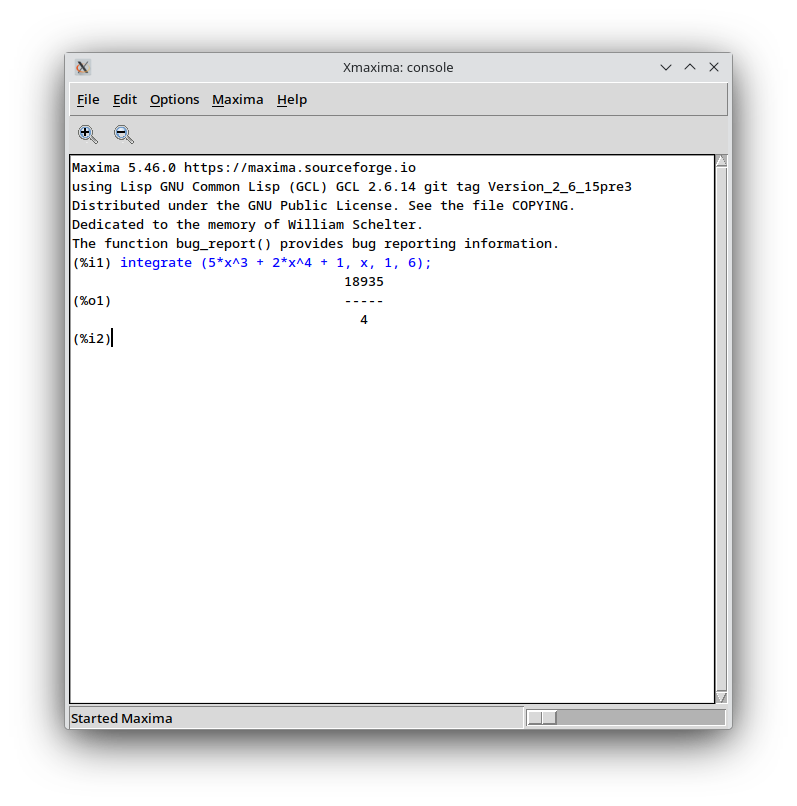
(%i1) integrate (5*x^3 + 2*x^4 + 1, x, 1, 6);
                                  18935
(%o1)                             -----
                                    4
(%i2)


f(x) = 5*x^3 + 2*x^4 + 1

f'(x) = 15*x^2 + 8*x^3
f'(x) = 0

Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) integrate (5*x^3 + 2*x^4 + 1, x, 1, 6);
                                  18935
(%o1)                             -----
                                    4
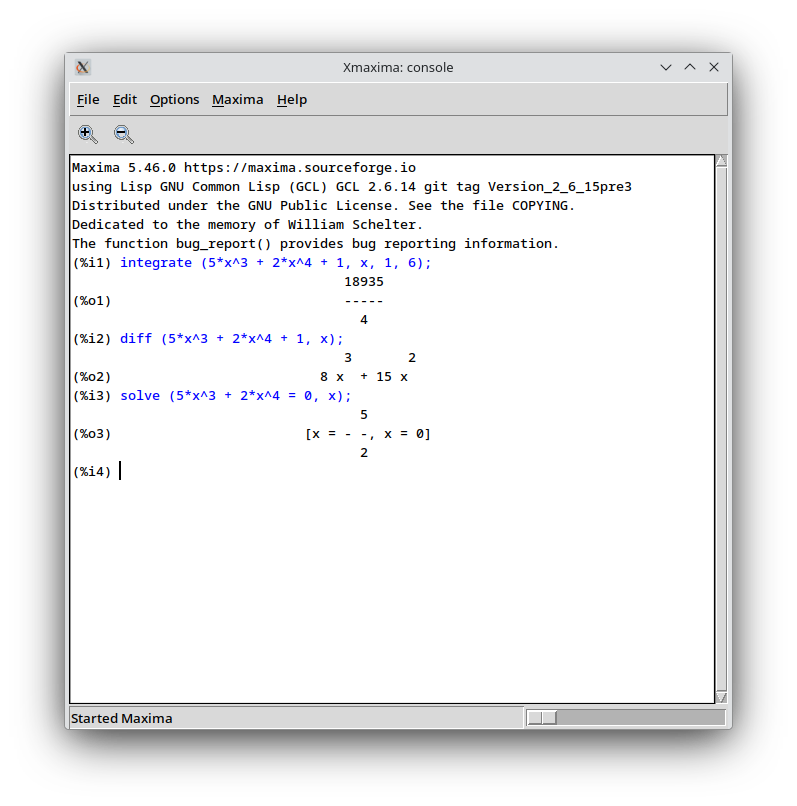
(%i2) diff (5*x^3 + 2*x^4 + 1, x);
                                  3       2
(%o2)                          8 x  + 15 x
(%i3) solve (5*x^3 + 2*x^4 = 0, x);
                                    5
(%o3)                        [x = - -, x = 0]
                                    2
(%i4)

Hier war ein fehler

(%i4) diff (5*x^3 + 2*x^4, x);
                                  3       2
(%o4)                          8 x  + 15 x
(%i5) solve (8*x^3+15*x^2 = 0, x);
                                   15
(%o5)                       [x = - --, x = 0]
                                   8

Falsche Gleichung

f(x) = 5*x^3 + 2*x^4 + 1

f'(x) = 15*x^2 + 8*x^3
f”(x) = 30*x + 24*x^2

f”(-15/8) = 30*(-15/8) + 24*(-15/8)^2 = 225/8
f”(0) = 30*(0) + 24*(0)^2 = 0

Maxima 5.46.0 https://maxima.sourceforge.io
using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) integrate (5*x^3 + 2*x^4 + 1, x, 1, 6);
                                  18935
(%o1)                             -----
                                    4
(%i2) diff (5*x^3 + 2*x^4 + 1, x);
                                  3       2
(%o2)                          8 x  + 15 x
(%i3) solve (5*x^3 + 2*x^4 = 0, x);
                                    5
(%o3)                        [x = - -, x = 0]
                                    2
(%i4) diff (5*x^3 + 2*x^4, x);
                                  3       2
(%o4)                          8 x  + 15 x
(%i5) solve (8*x^3+15*x^2 = 0, x);
                                   15
(%o5)                       [x = - --, x = 0]
                                   8
(%i6) diff (8*x^3+15*x^2, x);
                                   2
(%o6)                          24 x  + 30 x
(%i7) 30*(-15/8) + 24*(-15/8)^2;
                                   225
(%o7)                              ---
                                    8
(%i8)

#include <stdio.h>
#include <time.h>
#include <stdlib.h>

void expr (void);
void term (void);
void fact (void);

int main  (void) {
    time_t t;

    srand ((unsigned)time (&t));
    expr ();
return 0;
}

void expr (void) {
        term ();
        if (rand () % 2) {
            printf (" + ");
            expr ();
        }
return;
}
void term (void) {

        fact ();
        if (rand () % 2) {
            printf (" * ");
            term ();

    }
return;
}
int count = 0;
void fact (void) {
    if ((rand () % 2) && (count < 3)) {
        printf ("(");
        expr ();
        printf (")");
        count++;
    }
    else
        printf ("%i*x^%i", rand() % 8, rand () % 8);
return;
}

das geht noch gerade so

2*x^1 + (((4*x^3 + ((6*x^3 + 3*x^6))) + 7*x^1) + 2*x^1 * 3*x^3)

oder

6*x^7 * ((((5*x^1 * 0*x^0) * (((6*x^4 * 2*x^0 * 4*x^2 * 1*x^3))) * 7*x^6 * 0*x^2 + 5*x^4 * 1*x^5 + 1*x^2 + 7*x^6) * 4*x^3) * 1*x^4 * 5*x^3) * 1*x^4 + 3*x^5 + 2*x^0 * 0*x^2 * 0*x^2